Breaking Erlang Maps #2
This is part 2 in my work on using QuickCheck for Erlang to find errors in maps. I assume the reader is familiar with the first part, though I’ll start with a quick recap.
From where we came
In the first part, we built a generator which could generate data to put into maps. When we request something of type map_term(), we get a random term we can push into a map. We also have ways to create maps out of map terms.
We showed simple stateless tests for maps, including one which found a bug in 17.4.1 with respect to binary_to_term/1 and term_to_binary/2.
QuickCheck State Machines
To write stateful models, we will use QuickCheck’s state machine features. In these tests, we run the test as a state machine “one level up”. That is, we will use the state machine to generate random commands we can execute towards a map. And we will use generators from part #1 to generate arguments to these commands.
The reason we need a state machine is that some commands might only be eligible in certain states. Furthermore, the response from a command might depend on what state we are in — that is, what commands we already executed. Suppose we execute
maps:is_key(K, Map).
for a generated key K. This will return true, if the key is in the map, and false otherwise. But this result depends on what we already put inside the map and hence what commands we already run towards the map. This is why we need a model where a state machine keeps track of what is inside the map so we can check the response correctly.
Our strategy for the model is this: we define a model state where a field, ‘contents’, represents the underlying map as a list of K/V pairs. Suppose that the map is the following:
Map = #{ 123 => 42, sand => "hello" }
then the model will be:
State = #state { contents = [{123, 42}, {sand, "hello"}] }
If we then execute the command maps:put(5, 1, Map), we update the contents of the state correspondingly:
Cs = State#state.contents,
State#state { contents = Cs ++ [{5, 1}] }
Of course replacing an existing K/V pair if needed through, e.g., the equivalent of a lists:keyreplace/4.
We aim for the model state to correctly track the underlying map precisely, so we can answer any query on the map correctly, like for the is_key/2 example above.
Here is the simplified property of ‘maps_eqc’:
prop_map() ->
?SETUP(fun() ->
{ok, Pid} = maps_runner:start_link(),
fun() -> exit(Pid, kill) end
end,
?FORALL(Cmds, commands(?MODULE),
begin
maps_runner:reset(),
{H,S,R} = run_commands(?MODULE, Cmds),
pretty_commands(?MODULE, Cmds, {H,S,R}, R == ok)
end)).
The property beings with a ?SETUP phase. It starts a separate process, the ‘maps_runner’. This is a gen_server which holds the state of the map in between calls. When we want to call, is_key/2 on the map, we call the maps runner:
is_key(K) ->
maps_runner:is_key(K).
note we don’t have to supply the map since the‘maps_runner’ keeps track of the internal map state for us. The ‘maps_runner’ implements all the commands in the ‘maps’ module in this manner, tracking a map internally and returning the result of executing a command back to the caller.
Next we have ?FORALL(Cmds, commands(?MODULE), …) which is the first phase in a state-machine model. We generate a random set of commands, where the command rules are in ?MODULE (in this case ?MODULE = maps_eqc). QuickCheck will look for commands in the module and then build up a sequential set of commands by executing the state machine symbolically.
Now, with a specific set of commands in hand, we reset the ‘maps_runner’ so it has an empty map as contents. The next call, run_commands(?MODULE, Cmds) executes the state machine in dynamic mode, where the commands are replayed against the real system. It returns a History, a final State and a final Result. The final line in the property verifies that the result is ‘ok’ and will pretty-print the error if it is not.
The non-simplified version of the property looks like this:
prop_map() ->
?SETUP(fun() ->
{ok, Pid} = maps_runner:start_link(),
fun() -> exit(Pid, kill) end
end,
?FORALL(Cmds, more_commands(2, commands(?MODULE)),
begin
maps_runner:reset(),
{H,S,R} = run_commands(?MODULE, Cmds),
collect(eqc_lib:stem_and_leaf('Final map size'),
model_size(S),
collect(eqc_lib:stem_and_leaf('Command Length'),
length(Cmds),
aggregate(with_title('Commands'), command_names(Cmds),
aggregate(with_title('Features'), call_features(H),
pretty_commands(?MODULE, Cmds, {H,S,R}, R == ok)))))
end)).
It generates longer command sequences through invocation of more_commands/2, and it collects/aggregates statistics about a run. This allows us to look at the histogram of several runs so we can see if we cover all commands, or if final map sizes are too small. Statistics generation is often important in order to answer the question “did we cover all possibilities?”
Symbolic/Dynamic execution
It is important to stress how the system executes. We first generate commands, symbolically, without even invoking the system-under-test (SUT). Then, once we have a valid command sequence, we replay it against the SUT by executing the system in dynamic mode. It is only here we learn what the system does.
In particular, because we don’t invoke the SUT while generating commands,
We can’t use the concrete result of executing a command from the SUT to guide command generation.
At most, we can record that the SUT returns an opaque value, which we can store, but we can’t scrutinize the contents of that value. So all command generation has to rely on the model, and the model only. A common mistake by newcomers is to intermingle the symbolic/dynamic execution modes and this won’t work. When writing models, it is important to understand which parts of the model executes in symbolic mode, which executes in dynamic mode, and which executes in both. To illustrate what is going on, we can use this diagram:
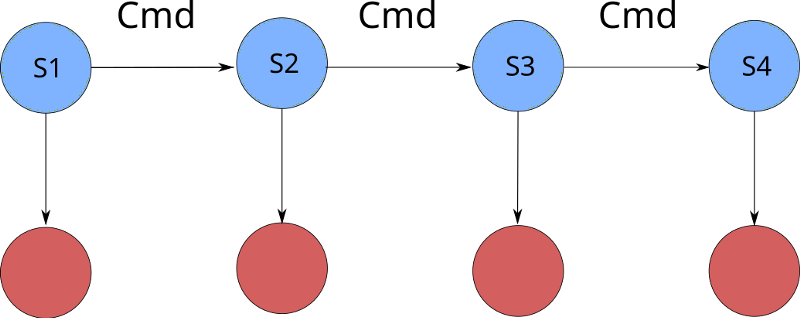
What happens first is that the blue states S1, …, S4 are generated. Each state is generated by figuring, at random, what command Cmd to run and then calculate the next (blue) model state based on the command. Once we have the blue chain, we run the system again, but now we make a call to the SUT at each state, depicted by the red circles. Each call to the SUT is associated with a postcondition. This checks if the real return value from the SUT is in correspondance with the model.
In our model, we can always calculate an expected return value from the model state. So we can handle all postconditions with a common postcondition:
postcondition_common(S, Call, Res) ->
eq(Res, return_value(S, Call)).
That is, in a given state, S, executing a Call with return value Res, we expect the result to be the same as the calculated return_value with respect to the state and the call executed.
is_key/1
The commands in the model is written in the so-called grouped style where an Erlang parse transformation reads the file and alters it before the compiler gets its hands on it. The grouped style is nice because it groups a given command so data pertaining to that command is close. There is an older, transposed format, which is much harder to read, and if you look at older models you may see it. They are equivalent and the parse transform transforms one to the other, essentially.
Let us start with a simple command, is_key, which checks if a key is present in the map and returns a boolean value:
is_key(K) ->
maps_runner:is_key(K).
This defines the command to run. It simply calls through to the maps_runner.
is_key_args(#state { contents = C }) ->
frequency(
[{10,
?LET(Pair, elements(C), [element(1, Pair)])} || C /= [] ] ++
[{1, ?SUCHTHAT([K], [map_key()], find(K, 1, C) == false)}]).
The grouped style parse transformation understands functions ending in certain code words and treads the specially. In this case COMMAND_args/1 is a generator for the arguments to COMMAND. Here, we are generating commands with a certain frequency. We are generating elements which are already present in the map. But we have wrapped this as a list comprehension which makes sure this only gets generated if there are elements in the contents/map in the first place. If the map is currently empty, this line, with frequency 10, will never be genereated.
The ?SUCHTHAT line constructs a map_key() which is not present in the current contents. The frequency ensures that if there are keys in the map, it is more likely to generate requests for those keys. But once in a while, we want a key which is not there, to check for negative elements.
Such positive/negative testing is common in QuickCheck models. We want to check for both Type I and Type II errors: false positives and false negatives. So we generate both kinds. Checking what is present is rather easy:
is_key_return(S, [K]) ->
member(K, S).
%% The following two functions are helpers:
member(K, #state { contents = C }) ->
member(K, 1, C).
member(_T, _Pos, []) -> false;
member(T, Pos, [Tup|Next]) ->
case element(Pos, Tup) =:= T of
true -> true;
false -> member(T, Pos, Next)
end.
The expected return from is_key/1 is simply a membership on the models list. We have to write our own variant because the lists modules keyfind/3 function considers 0 and 0.0 to be equivalent and we don’t want that here.
How can we be sure our test case actually tests both positive and negative variants of is_key/1? To answer the question, we can use a features function,
is_key_features(_S, [_K], true) ->
["R001: is_key/2 on a present key"];
is_key_features(_S, [_K], false) ->
["R002: is_key/2 on a non-existing key"].
which is run in dynamic execution of the state machine. It defines a list of features that the test case hits. So if the function returns ‘true’ we know we have hit feature R001 and if it returns false, we know we have hit feature R002. The full model has close to 40 features it checks for. And it provides statistics as to how often features are hit.
put/2
while is_key/1 is a query-style command that won’t alter the model state, we have not seen how to write a case where the model state is altered. A good simple example of such a state is the put/2 command:
put(Key, Value) ->
maps_runner:put(Key, Value).
Generating arguments for put/2 is very straightforward, since we already have generators for keys and values:
put_args(_S) ->
[map_key(), map_value()].
However, putting a new K/V pair into the map alters the state. To track this, we define a _next/3 function which tracks that the map got new contents, or overwrote existing content:
put_next(#state { contents = C } = State, _, [K, V]) ->
State#state { contents = add_contents(K, V, C) }.
The _next/3 state is special because it is executed both in symbolic and in dynamic mode. First it is used to build up the command model, and then it is used to understand what the results of replaying the model against the SUT is.
The return value of a put command is the new map. To check this, we use the state and the new K/V pair to generate a map which can be tested for equality:
put_return(#state { contents = C}, [K, V]) ->
maps:from_list(add_contents(K, V, C)).
Note: The input to return is the state prior to executing the command. So we have to track that the new K/V pair was added to that state before constructing the expected map. Many QuickCheck commands runs under this assumption in state machine models[0].
Finally, we define the feature set of putting data into the map:
put_features(S, [K, _Value], _Res) ->
case member(K, S) of
true -> ["R003: put/3 on existing key"];
false -> ["R004: put on a new key"]
end.
Preconditions
The full model contains 24 commands, hence we won’t explain all of them. Most of them are similar to the above, albeit they work for other ‘maps’ commands. A commonality among commands are that they can always be executed. There are no conditional limit that says “in this state, you can’t execute command X”. Hence, the model doesn’t really use the stateful features up to this point. But there is something I call meta-commands in the model as well.
A meta-command encodes a property of maps which can’t be tested as part of calling a ‘maps’ function. In functional languages, maps have to be persistent. That is, if we remember a version of the map in a variable, and later refer to that older version, then it should persistent. Newer data must not interfere in a destructive way.
We handle this, by extending the state of‘maps_eqc’ to also contain a persistence table:
-record(state,
{ contents = [] :: list_map(), %% The current contents
persist = [] :: list({reference(), list_map()}) %% Remembered
}).
And then we define a command which can“remember” a map in a given state:
remember(Ref) ->
maps_runner:remember(Ref).
remember_args(_S) -> [make_ref()].
remember_next(#state { contents = Cs,
persist = Ps } = State, _, [Ref]) ->
State#state { persist =
lists:keystore(Ref, 1, Ps, {Ref, Cs}) }.
remember_return(_S, [_Ref]) ->
ok.
Now, the rule is, that if we at any point“recall” one of the remembered states, it should return exactly the same data as the remembered version in the model. But note, that in order to “recall” a map we must first have it remembered. That is, we can only recall, if a “remember” were among the earlier commands. This is typical conditional command generation in state machine models. We encode this as a precondition on the model state:
recall(Ref) ->
maps_runner:recall(Ref).
%% Can only recall when there are persisted maps to recall
recall_pre(#state { persist = Ps }) -> Ps /= [].
This makes the recall/1 command illegal in any state where there is no persisted map. And the symbolic command generator will avoid generating such a command. Defining the _args/1 function is straightforward, since we can assume there is something in the persistence table to pick:
recall_args(#state { persist = Ps }) ->
?LET(Pair, elements(Ps),
[element(1, Pair)]).
recall_pre(#state { persist = Ps}, [Ref]) ->
lists:keyfind(Ref,1,Ps) /= false.
Note there are two precondition commands. The _pre/1 command is called before argument generation, and _pre/2 is called after. The second precondition command helps with shrinking, which is why it is here. It makes sure we can’t shrink away a reference we are going to use later. Having both preconditions can speed up command generation a lot if it is expensive the generate arguments, which is why you have the _pre/1 variant.
The return and feature set is as expected:
recall_return(#state { persist = Ps }, [Ref]) ->
{Ref, Cs} = lists:keyfind(Ref, 1, Ps),
{ok, maps:from_list(Cs)}.
recall_features(_S, _, _) ->
["R038: Recalled a persisted version of the map successfully"].
Map and Fold
The full model is more involved:
-
It uses a “become” command to become and older version of the map to test persistence fully.
-
It roundtrips maps back and forth between processes to test for messaging correctness.
-
It populates empty maps to verify that from_list/1 works correctly.
-
It uses weight/2 to make map-altering commands more likely than query-commands. The idea that if a query goes wrong, it is probably due to some alteration, so we check alteration more than query-style commands.
An interesting thing happens with checking map and fold though. When you want to check maps:map/2, you need a function which works on any map term and returns deterministic values. It turns out QuickCheck has such a function and can generate them for us. Calling function2(int()) generates a function of type (term(), term()) -> int() which behaves deterministically: given the same input, it returns the same output. Hence testing map is easy:
map_args(_S) ->
?LET(F, function2(map_value()), [F]).
and then we can just check the expected return of calling maps:map(F, Map):
map_return(#state { contents = Cs }, [F]) ->
NCs = lists:map(fun({K, V}) -> {K, F(K,V)} end, Cs),
maps:from_list(NCs).
For fold, however, one might think it is much harder. Not so! It turns out that one function is enough:
fold() ->
Res = maps_runner:fold(fun(K, V, L) -> [{K, V} | L] end, []),
sort(Res).
This fold function “blits” the map as were it a list. If we sort that list, we have a unique canonical representation of the map. If we duplicate a K/V pair, or miss one, in the maps:fold/3 implementation, this function will find it. Hence, testing fold is, surprisingly, trivial:
fold_args(_S) -> [].
fold_return(#state { contents = Cs }, _) ->
sort(Cs).
fold_features(_S, _, _) ->
["R027: traverse over the map by fold/3"].
Running the model
Executing this model on 18.0-rc1 + patches is currently safe:
2> eqc:module(maps_eqc).
Starting Quviq QuickCheck version 1.33.3
(compiled at {{2015,2,9},{14,18,24}})
Licence for Private Licences reserved until {{2015,3,31},{19,5,8}}
prop_map: ....................................................................................................
OK, passed 100 tests
Final map size
Stem | Leaf
----------------
0 | 000000000111122222233344555677899999
1 | 0022666788
2 | 0122567899
3 | 0122556
4 | 124888
5 | 1123559999
6 | 12
7 | 23588
8 | 128
9 | 269
10 | 37
11 | 34599
12 | 7
Here we see the output from the Steam & Leaf plots[1]. It tells us there were exactly 3 maps around size 80–90: 81, 82, and 88. The largest map where of size 127. The next section gives us the command size:
Command Length
Stem | Leaf
----------------
0 | 0111111111222222333333344445555566777788889999
1 | 011223344445555666778899
2 | 00012223458889999
3 | 03489
4 | 1125
5 | 9
6 | 4
7 | 04
Most command sequences are rather small, but there are serious command sequences in between. Had we requested a budget of an hour for the test, we would have a much longer command sequences and a completely different spread. 100 tests, as run here, is good while wanting fast feedback when developing, but before release you probably want a good night of extensive test runs.
Next section breaks down commands:
Commands
9.9% {maps_eqc,remove,1}
9.8% {maps_eqc,put,2}
9.6% {maps_eqc,merge,1}
9.5% {maps_eqc,update,2}
6.2% {maps_eqc,populate,2}
5.3% {maps_eqc,to_list,0}
4.9% {maps_eqc,values,0}
4.8% {maps_eqc,m_get,1}
4.4% {maps_eqc,keys,0}
4.3% {maps_eqc,remember,1}
4.3% {maps_eqc,find,1}
4.1% {maps_eqc,is_key,1}
3.9% {maps_eqc,fold,0}
3.8% {maps_eqc,size,0}
3.6% {maps_eqc,m_get_default,2}
2.4% {maps_eqc,roundtrip,0}
2.4% {maps_eqc,extract,0}
2.0% {maps_eqc,without_q,1}
2.0% {maps_eqc,with_q,1}
1.7% {maps_eqc,recall,1}
0.4% {maps_eqc,without,1}
0.4% {maps_eqc,with,1}
0.3% {maps_eqc,become,1}
The weighting makes sure altering commands are more common than query style commands. The “become” command, which essentially resets the map back to an older version is deliberately made unlikely as to test for other things more frequently.
The keen eye will note that map/2 is disabled for this test run. The reason is that 0.0 and 0.0/-1 causes trouble for the function generators, so we are currently running without it.
Finally, we list the covered features:
Features
9.9% {{maps_eqc,merge,1},"R019: Merging two maps"}
9.0% {{maps_eqc,put,2},"R004: put on a new key"}
7.7% {{maps_eqc,update,2},"R015: update/3 on an existing key"}
7.7% {{maps_eqc,remove,1},"R011: remove/2 of present key"}
5.4% {{maps_eqc,to_list,0},"R013: to_list/1 called on map"}
5.0% {{maps_eqc,values,0},"R014: values/1 called on map"}
4.5% {{maps_eqc,keys,0},"R010: Calling keys/1 on the map"}
4.1% {{maps_eqc,m_get,1},"R023: get on a successful key"}
4.0% {{maps_eqc,fold,0},"R027: traverse over the map by fold/3"}
3.5% {{maps_eqc,is_key,1},"R001: is_key/2 on a present key"}
3.3% {{maps_eqc,populate,2},"R017: populating an empty map with from_list/1"}
3.2% {{maps_eqc,find,1},"R021: find on an existing key"}
3.0% {{maps_eqc,populate,2},"R018: populating an empty map with put/2"}
2.8% {{maps_eqc,m_get_default,2},"R024: get/3 on an existing key"}
2.5% {{maps_eqc,remove,1},"R012: remove/2 of non-present key"}
2.5% {{maps_eqc,roundtrip,0},
"R037: Maps sent roundtrip through another process are reflexive"}
2.4% {{maps_eqc,extract,0},
"R036: Maps are consistent when sending them to another process"}
2.1% {{maps_eqc,update,2},"R016: update/3 on a non-existing key"}
2.0% {{maps_eqc,without_q,1},"R031: withtout/2 query on non-existing keys"}
1.9% {{maps_eqc,with_q,1},"R029: with/2 query on non-existing keys"}
1.8% {{maps_eqc,recall,1},
"R038: Recalled a persisted version of the map successfully"}
1.7% {{maps_eqc,size,0},"R007: size/1 on a 16+ map"}
1.4% {{maps_eqc,size,0},"R009: size/1 on a small non-empty map"}
1.2% {{maps_eqc,find,1},"R020: find on a non-existing key"}
1.1% {{maps_eqc,put,2},"R003: put/3 on existing key"}
0.9% {{maps_eqc,m_get_default,2},"R025: get/3 on a non-existing key"}
0.8% {{maps_eqc,m_get,1},"R022: get/2 on a non-existing key"}
0.8% {{maps_eqc,with_q,1},"R028: with/2 query on present keys"}
0.7% {{maps_eqc,without_q,1},"R030: withtout/2 query on present keys"}
0.7% {{maps_eqc,size,0},"R006: size/1 on a 64+ map"}
0.7% {{maps_eqc,is_key,1},"R002: is_key/2 on a non-existing key"}
0.5% {{maps_eqc,with,1},"R033: with/2 on non-existing keys"}
0.4% {{maps_eqc,without,1},"R035: withtout/2 on non-existing keys"}
0.3% {{maps_eqc,become,1},
"R039: Refocus and \"become\" an old version of the map"}
0.2% {{maps_eqc,without,1},"R034: withtout/2 on present keys"}
0.2% {{maps_eqc,with,1},"R032: with/2 on present keys"}
0.1% {{maps_eqc,size,0},"R008: size/1 on an empty (0) map"}
0.1% {{maps_eqc,size,0},"R005: size/1 on a 128+ map"}
[]
We can see for this run, that there is not much confidence in calls to maps:size/1, but most of the calls have a nice spread.
Limits of the model
Are maps now correct in 18.0-rc1 + patches? No. We have established confidence that small maps, those with few elements, are relatively safe due to the model. But we have not covered all of what HAMT maps entail. In the HAMT, we hash values and collisions on hashes is a central thing. The hash space is vast, at least 32 bit in size, so the chance of getting a collision in a small map is fairly low. Björn-Egil Dahlberg has found and fixed bugs with collisions which this model did not find, because he needed maps in the vicinity of 150.000 elements. At that size, collisions are more common and so it is possible to find bugs. The current QuickCheck model generates elements close to the size of 400 elements at most, so the birthday paradox is not rolling the dice as we would like.
The author plans to run BEAM under coverage checking and then see what parts of the HAMT code isn’t hit with the above model. This can then guide the construction of ‘maps_large_eqc’ which can check such large maps with thousands of keys. Hopefully the two tests together will provide decent coverage of the HAMT code and weed out the remaining bugs, even for those maps which are large. Alternatively, I’ll weaken the hash function to collide almost everything.
We also expect the code around maps to change. Having a QuickCheck model which does random changes to maps is a help when this happens. Even for a small number of runs, it is a good verifier of obvious mistakes in code bases.
Also, a quick Cost/Benefit analysis says it took around 10 hours of work to build the model, and perhaps a bit more in “analytic thinking time”. Given its current coverage, it would have taken at least 100 hours writing unit tests with the same coverage. And it wouldn’t scale if a new command was added to the ‘maps’ module.
This post was based on commit ID 4344b287a4c98
[0] QuickCheck supports several different kinds of state machine models. One of these, the component model, can delimit internal state transitions, so complex transitions can be split into several smaller steps. But the statem model cannot.
[1] Stem and leaf plots are not part of QuickCheck, but is an extension present in jlouis/eqc_lib at Github. It also contains other useful helpers for QuickCheck models.